| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 경력기술서 첨삭
- 주가데이터
- 주요 파라미터
- 과제전형
- 파이썬
- 주식데이터
- 공공데이터
- 데이터 분석
- 하이퍼 파라미터
- 사이킷런
- 커리어전환
- 데이터사이언스
- 머신러닝
- 퀀트 투자 책
- 대학원
- 경력 기술서
- 자기소개서
- 코딩테스트
- AutoML
- 퀀트
- 데이터 사이언스
- sklearn
- 랜덤포레스트
- 판다스
- 데이터 사이언티스트
- 데이터분석
- pandas
- 하이퍼 파라미터 튜닝
- 데이터사이언티스트
- 이력서 첨삭
- Today
- Total
GIL's LAB
랜덤 포레스트(회귀)의 하이퍼 파라미터 튜닝 본문
이번 포스팅에서는 회귀를 위한 랜덤포레스트의 하이퍼 파라미터를 튜닝하는 방법에 대해 알아보겠습니다.
랜덤포레스트는 sklearn.ensemble.RandomForestRegressor를 이용해서 구현하겠습니다.
하이퍼 파라미터
sklearn.ensemble.RandomForestRegressor의 주요 하이퍼 파라미터(함수 인자)는 다음과 같습니다.
하이퍼 파라미터에 대한 설명은 scikit learn의 공식 문서를 참고해서 작성했습니다.
- n_estimators: 랜덤포레스트를 구성하는 결정나무의 개수로 기본값은 100입니다.
- criterion: 결정 나무의 노드를 분지할 때 사용하는 불순도 측정 방식으로, 'mse', ',mae' 중 하나로 입력합니다. 최근 버전(1.2)에서는 각각 "squared_error"와 "absolute_error"로 입력합니다.
- max_depth: 결정 나무의 최대 깊이입니다. 만약 None으로 입력하며 잎 노드가 완전 순수해지거나 모든 잎 노드에 min_samples_split_samples보다 적은 수의 샘플을 포함할 때까지 결정 나무를 학습시킵니다.
- max_features: 결정 나무를 분지할 때 고려하는 특징 수(int) 혹은 비율(float)입니다. 기본값은 sqrt로 특징 개수에 루트를 씌운 값입니다.
- max_samples: 각 결정 나무를 학습하는 데 사용할 샘플의 개수(int) 혹은 비율(float)입니다.
실험 데이터
실험에 사용할 데이터는 KEEL에서 수집했으며, 수집한 데이터 목록은 다음과 같습니다.
- autoMPG8
- baseball
- concrete
- dee
- diabetes
- ele-1
- ele-2
- forestFires
- friedman
- laser
- machineCPU
- mortgage
- plastic
- stock
- treasury
- wankara
- wizmir
수집한 데이터는 행의 개수가 2000개 미만인 작은 데이터입니다.
데이터가 크면 이 실험 결과를 그대로 적용할 수 없을 수 있습니다.
실험 방법
각 데이터마다 1천번의 랜덤 샘플링을 수행해서 하이퍼 파라미터에 따른 MAE를 측정합니다.
각 하이퍼 파라미터를 샘플링하는 확률 분포는 다음과 같이 정의했습니다.
- n_estimator: 로그유니폼(하한: 10, 상한: 1000, 샘플링 후 int로 변환)
- criterion: mse와 mae를 각 50%의 확률로 선택
- max_depth: 로그유니폼(하한: 3, 상한: 50, 샘플링 후 int로 변환)
- max_features: 유니폼(하한: 0.2, 상한: 1.0)
- max_samples: 유니폼(하한: 0.2, 상한: 1.0)
이렇게 측정한 데이터를 바탕으로 주요 하이퍼 파라미터와 그 범위를 식별하겠습니다.
실험 결과
데이터에 따른 성능 범위
데이터별로 MAE의 편차가 크므로, 데이터마다 MAE를 0과 1사이로 표`준화했습니다. 이를 n_MAE라 쓰겠습니다.
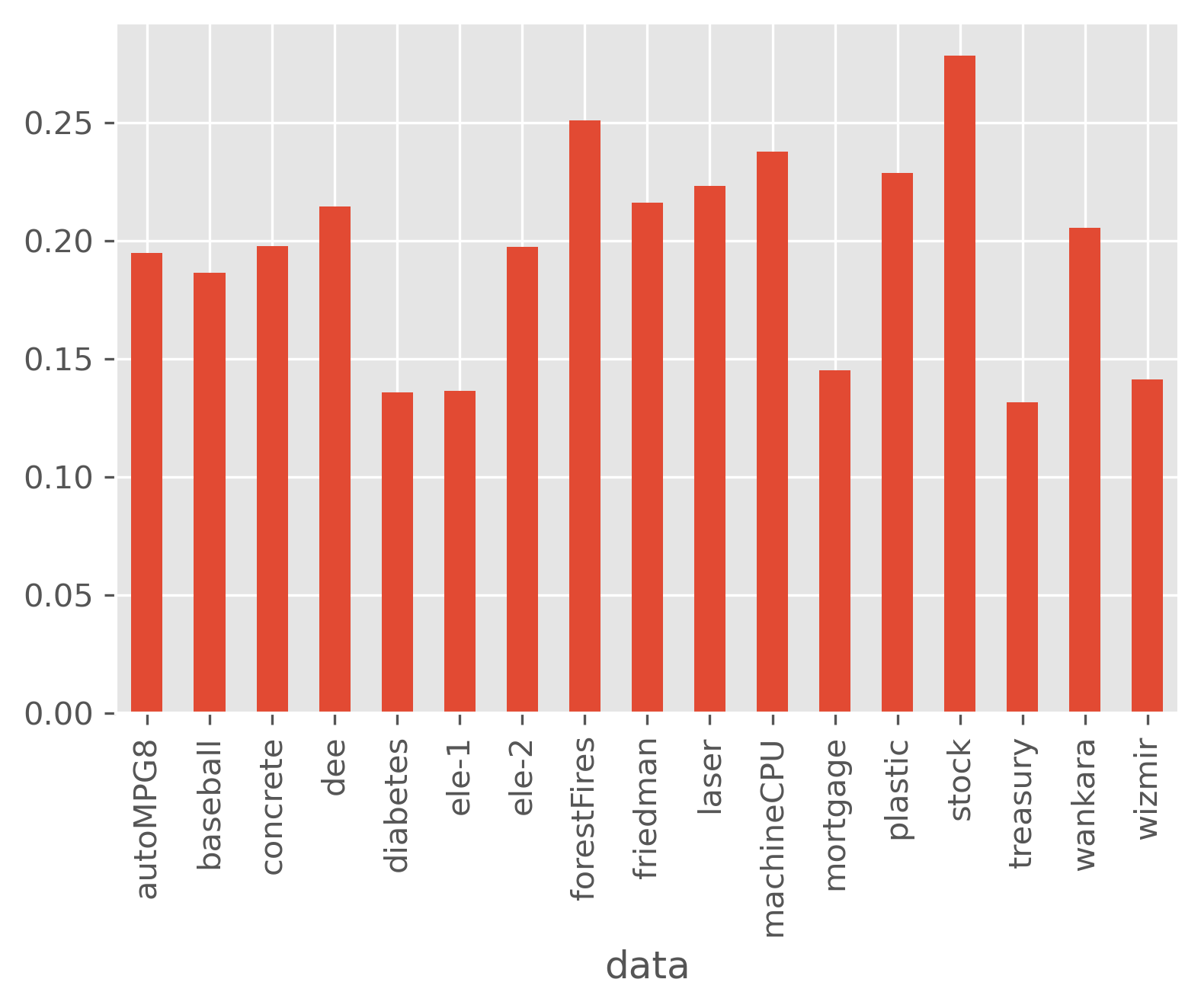
데이터별 n_MAE의 표준 편차는 다음과 같습니다.
상대적으로 편차가 크지 않은 데이터인 diabetes, ele-1과 같은 데이터도 있고, 편차가 큰 stock 같은 데이터도 있습니다.
편차가 작은 데이터는 하이퍼 파라미터 튜닝이 그다지 필요하지 않고, 편차가 큰 데이터는 하이퍼 파라미터 튜닝이 필수적이라고 할 수 있습니다.
문제는 실험 전에는 이런 차이가 있는지를 알기 어렵다는 것입니다.
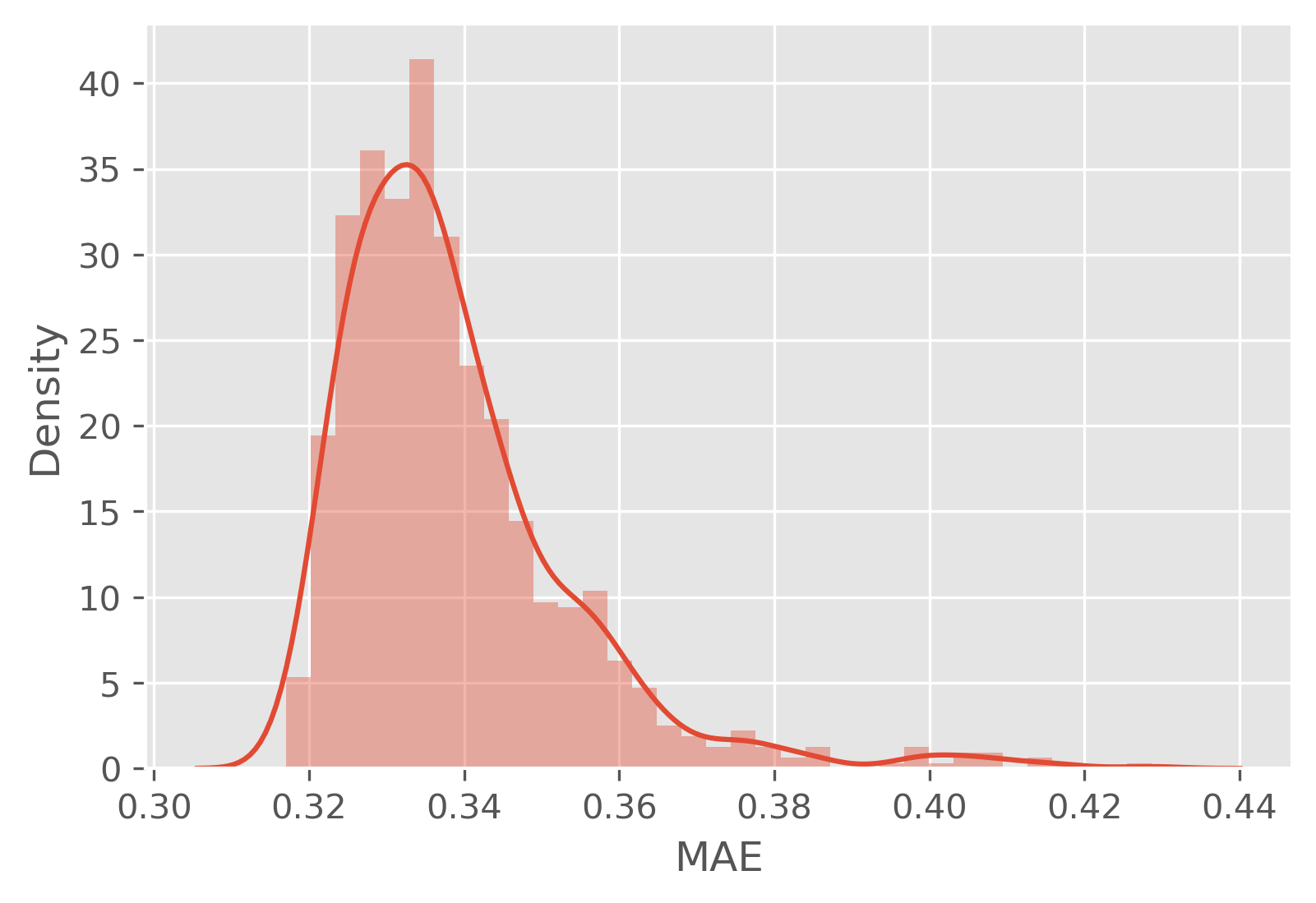
(참고 1) n_MAE의 편차가 작은 데이터(diabetes)의 MAE의 분포는 다음과 같습니다.
(참고 2) n_MAE의 편차가 큰 데이터(stock)의 MAE의 분포는 다음과 같습니다.

n_estimators에 따른 성능 분포
데이터별로 n_estimators에 따른 MAE의 평균을 구해보겠습니다.
다른 인자의 영향을 최소화하기 위해 n_estimators를 [10, 20), [20, 30)과 같이 구간화하고 각 구간에 속하는 평균 MAE를 사용하겠습니다.
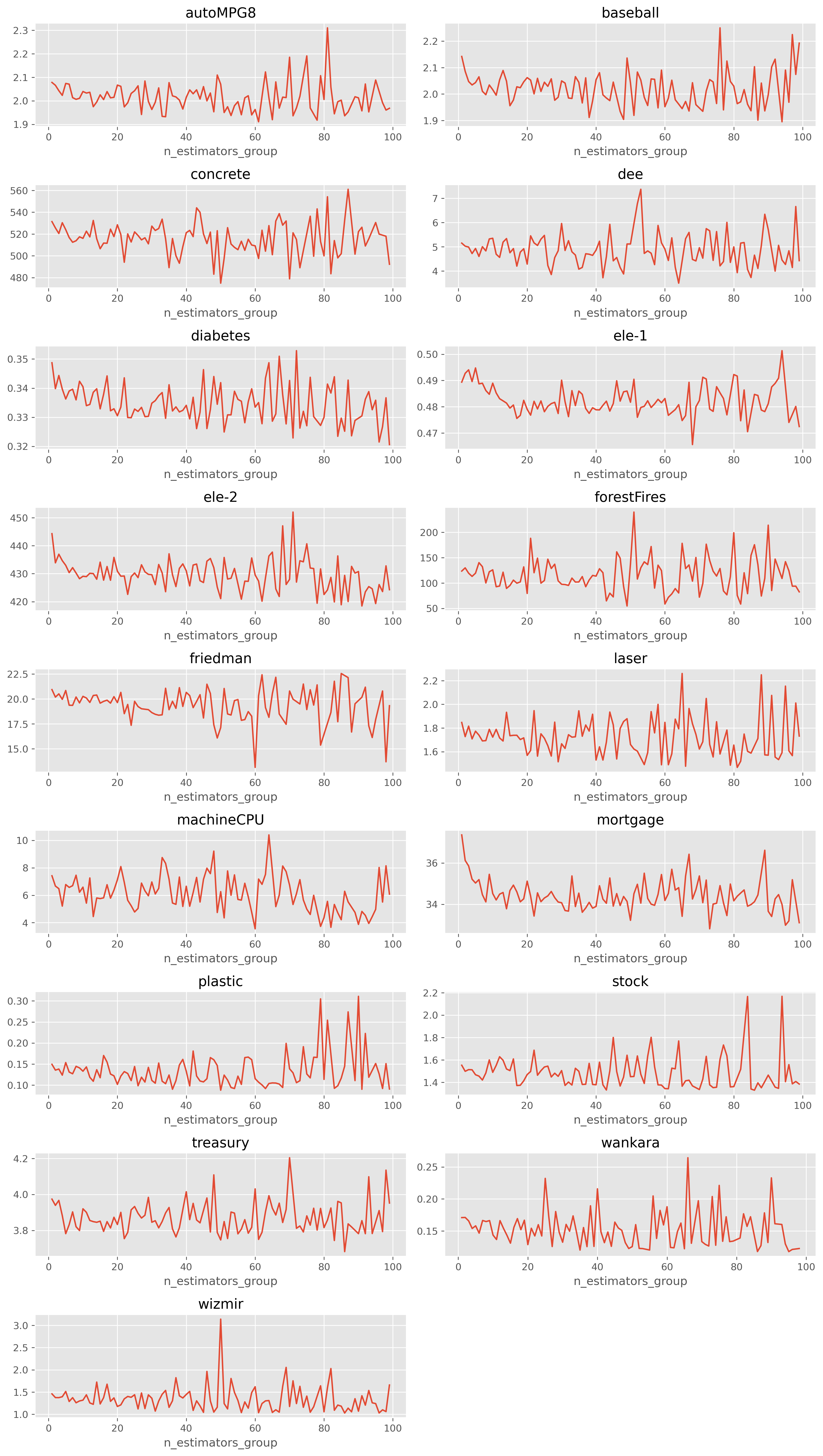
이진 분류와는 다르게 어느 정도에서 수렴하는 패턴이 보이지 않고, 값에 따라 변동이 꽤 있습니다.
그렇기 때문에 하이퍼 파라미터 튜닝이 반드시 필요합니다.
다만 근처의 값은 유사함을 알 수 있으며, 의외로 트리 수가 많아질수록 오차가 큰 경우도 제법있습니다.
따라서 다음과 같은 튜닝 구간을 추천합니다: [50, 100, 150, 200, 400]
criterion에 따른 성능 분포
criterion에 따른 데이터별 n_MAE의 분포는 다음과 같습니다.
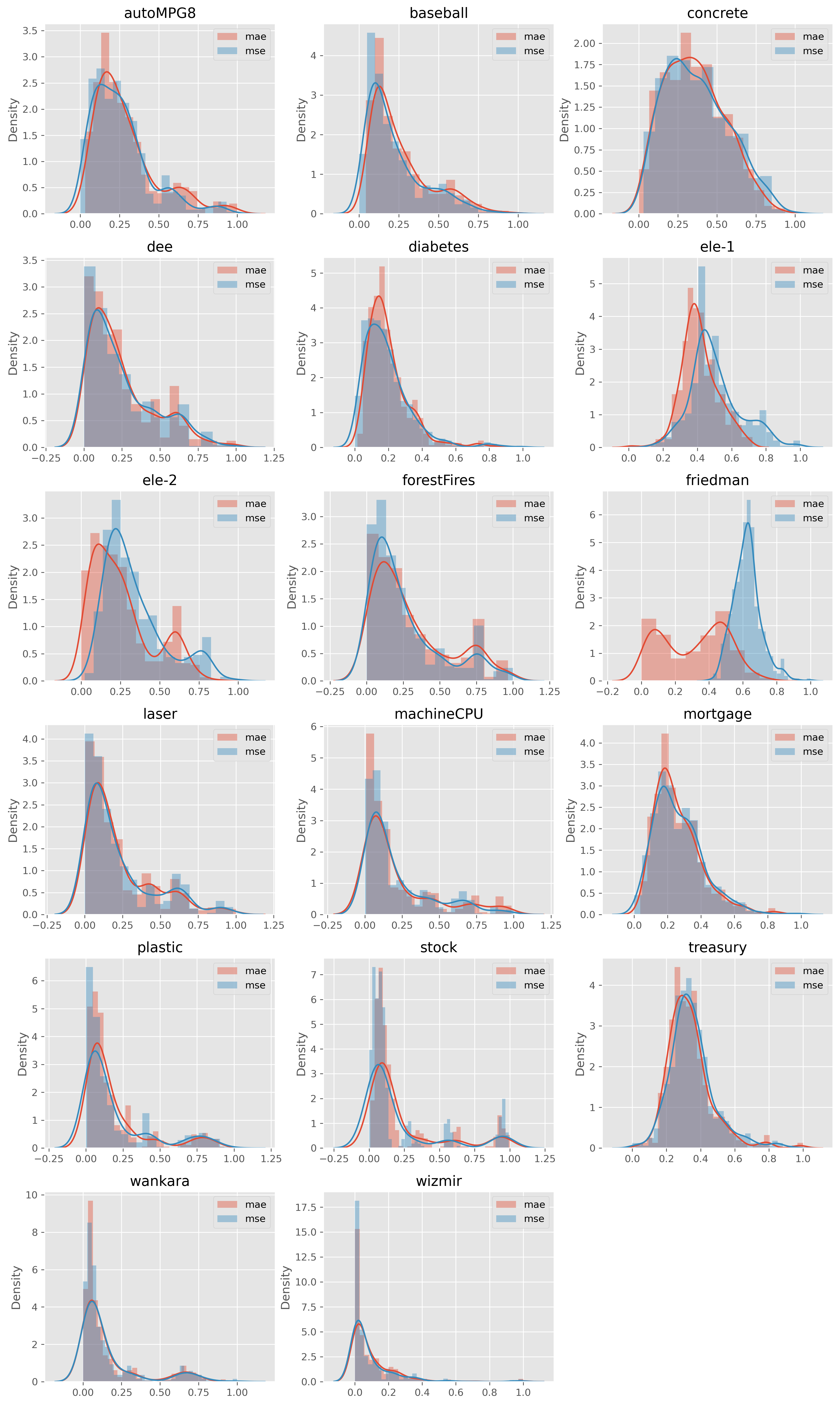
대부분 데이터에서는 큰 차이가 없었지만, 분류와는 다르게 criterion에 따라 차이가 있는 경우도 있었습니다.
예를 들어, friedman와 ele-1 데이터에 대해서는 mae가 더 적절했습니다.
따라서 시간적인 여건이 된다면 criterion을 튜닝하는 것이 좋아보입니다.
튜닝할 값도 두 개밖에 되지 않으므로 다른 하이퍼 파라미터에 비해 덜 부담이 된다고 할 수 있습니다.
max_depth에 따른 성능 분포
max_depth에 따른 성능 분포는 다음과 같습니다.

max_depth에 따른 성능 분포는 아래 두 가지 케이스로 구분할 수 있습니다.
(1) 특정 값에서 수렴하는 경우 (예: stock은 9부터 수렴함)
(2) 초기 값이 가장 크고 줄어들다 수렴하는 경우
수렴하는 이유는 max_depth가 어느 정도 수치 이상이 되면 분지할 것이 없어 나무의 깊이가 고정되기 때문입니다.
다시 말해, max_depth가 1000이든 10000이든 사실 같은 나무를 학습하게 될 것입니다.
감소하는 이유는 배깅을 한 샘플 데이터가 작아서 그렇습니다.
데이터에 상관없이 탐색 공간을 줄이고 싶다면 [5, 10, 15, 20] 정도에서 튜닝하는 것이 가장 좋아보입니다.
max_samples에 따른 성능 분포
그래프가 너무 지저분한 것을 방지하기 위해, 이동 평균(m = 10)을 적용하여 시각화했습니다.
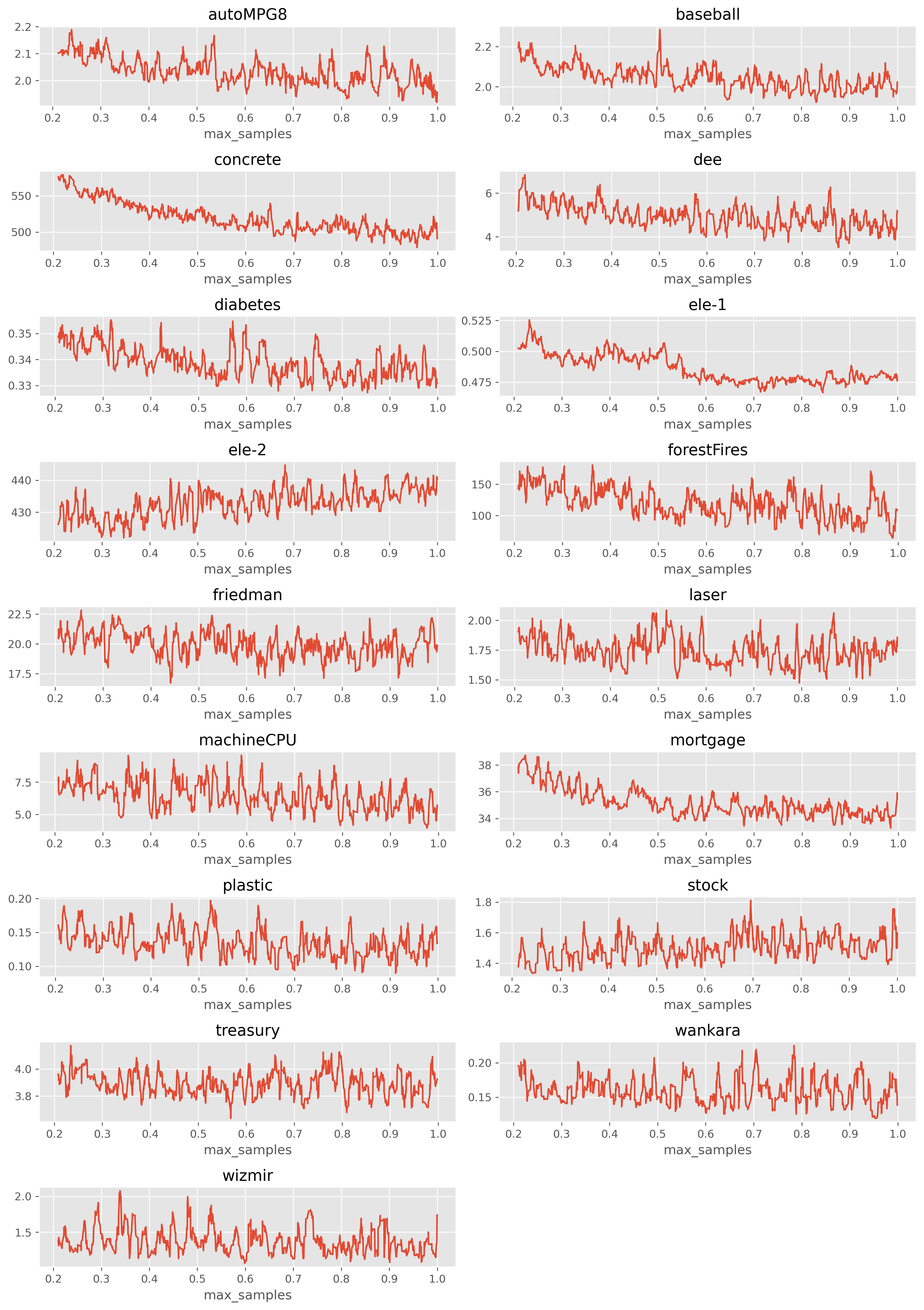
크게 보면 다음과 같이 두 가지 케이스로 구분할 수 있을 것 같습니다.
(1) max_samples가 증가함에 따라 MAE가 감소하는 케이스 (예: ele-1, concrete)
(2) max_samples와 크게 관련이 없는 케이스
max_samples에 따른 변동이 크지만 어느 정도 주기성이 보입니다.
주기성이 보이는 이유는 정확히는 모르겠습니다. 논리적으로 설명하기 어렵네요.
아무튼 주기성이 보이므로 매우 촘촘하게 탐색할 필요는 없어보입니다.
따라서 다음과 같은 탐색 범위를 추천합니다: [0.2, 0.4, 0.7, 0.8, 0.9, 1.0]
max_features에 따른 성능 분포
그래프가 너무 지저분한 것을 방지하기 위해, 이동 평균(m = 10)을 적용하여 시각화했습니다.
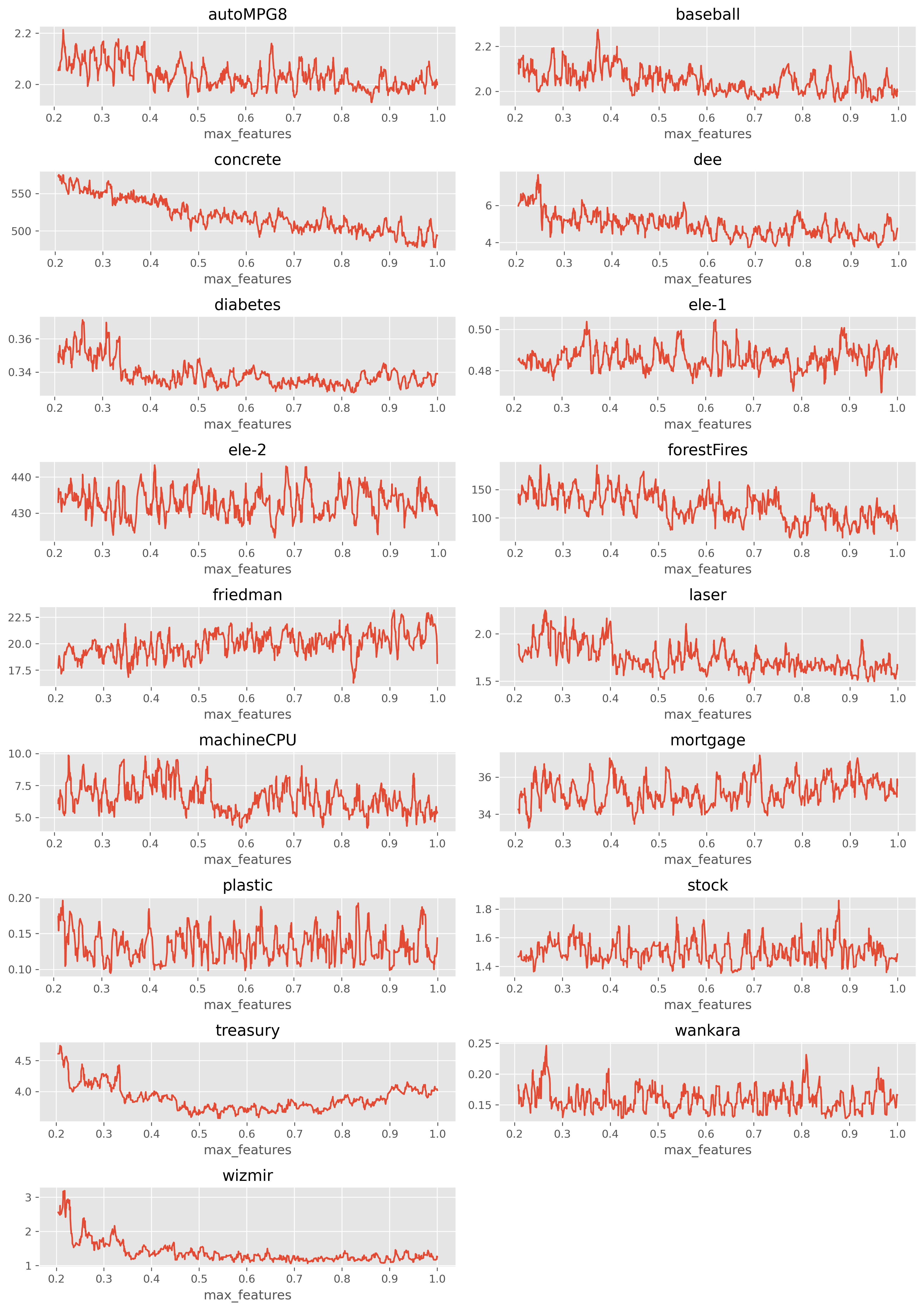
max_samples와 매우 유사한 경향을 보입니다.
따라서 다음과 같은 탐색 범위를 추천합니다: [0.2, 0.4, 0.7, 0.8, 0.9, 1.0]
데이터 분석 서비스가 필요한 분은 아래 링크로!
데이터사이언스 박사의 데이터 분석 서비스 드립니다. | 150000원부터 시작 가능한 총 평점 5점의 I
78개 총 작업 개수 완료한 총 평점 5점인 데이터사이언스박사의 IT·프로그래밍, 데이터 분석·시각화 서비스를 68개의 리뷰와 함께 확인해 보세요. IT·프로그래밍, 데이터 분석·시각화 제공 등 150
kmong.com
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| k-최근접 이웃의 k값 튜닝 방법 (0) | 2022.07.31 |
|---|---|
| 서포트 벡터 머신(이진 분류, rbf 커널)의 하이퍼 파라미터 튜닝 (0) | 2022.07.29 |
| 랜덤 포레스트(이진 분류)의 하이퍼 파라미터 튜닝 (0) | 2022.07.25 |
| 모델별 하이퍼 파라미터 튜닝 가이드라인 (0) | 2022.07.25 |
| 랜덤포레스트와 다중공선성 (0) | 2022.07.24 |



