| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 대학원
- 퀀트 투자 책
- 커리어전환
- 베이지안 최적화
- 퀀트
- 이력서 첨삭
- 경력 기술서
- 주식데이터
- pandas
- 하이퍼 파라미터 튜닝
- 머신러닝
- AutoML
- 파라미터 튜닝
- 데이터사이언스
- 코딩테스트
- 하이퍼 파라미터
- 판다스
- 사이킷런
- 데이터분석
- 경력기술서 첨삭
- 랜덤포레스트
- 데이터사이언티스트
- 주가데이터
- 파이썬
- 데이터사이언스학과
- 자기소개서
- 데이터 사이언스
- sklearn
- 데이터 사이언티스트
- 주요 파라미터
- Today
- Total
GIL's LAB
실험 11. 캘린더 효과 검증하기 (1) 요일 효과 본문
안녕하세요. 이번 포스팅에서는 대표적인 캘린더 효과 중 하나인 요일 효과를 검증해보겠습니다.
요일 효과
요일 효과 혹은 주말 효과란 월요일의 주가가 낮고 금요일의 주가가 높은 현상을 말합니다. 이러한 현상은 주말동안 발생했던 부정적인 내용의 소식이 월요일 주가에 영향을 끼치기 때문이라고 알려져있습니다. 그래서 월요일에 매수해서 금요일에 매도하기만 하면 잃지는 않는다는 속설까지 생겼고, 또 관련 기사도 많습니다 (아래 기사 참고)
https://biz.chosun.com/site/data/html_dir/2015/08/19/2015081904159.html
대상 종목
실험에 사용할 주가 데이터는 2016년 1월 1일 이전에 코스피와 코스닥에 상장된 모든 기업의 2016년 1월 1일부터 2021년 1월 1일까지 5개년 데이터로 한정하겠습니다.
실험 코드
1. 모듈 설치 및 불러오기
anaconda prompt에서 pip을 사용해 qspy 패키지를 설치해주겠습니다. 이 패키지에는 다양한 데이터가 포함되어 있기 때문에, 설치에 제법 오랜 시간이 걸립니다. 이미 설치한 분이라면 이 단계를 스킵해도 좋습니다.
pip install git+https://github.com/GilseungAhn/qspy.gitqspy에 대한 내용은 아래 링크에서 확인할 수 있습니다 (도움이 되었다면 하트부탁드립니다 :)
https://github.com/GilseungAhn/qspy
이제 주피터 노트북에서 필요한 모듈을 모두 불러오겠습니다.
# 필요 모듈 불러오기
from qspy import datasets
from qspy.analysis import calendar_effect
from qspy.validation import ror_buy_and_sell, ror_buy_and_hold
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
2. 데이터 준비
ListingDate 컬럼이 2016년 1월 1일 이전인 데이터를 stock_list에 다음과 같이 저장하겠습니다.
# 2016년 1월 1일 이전 코스피 혹은 코스닥에 상장된 모든 종목 정보를 stock_list에 저장
stock_list = datasets.load_stock_list(market = "all")
stock_list = stock_list.loc[stock_list['ListingDate'] < pd.to_datetime("2016-01-01")]
이제 stock_list에 속한 종목 코드를 기준으로 주가 데이터를 가져오겠습니다. 2016년 1월 1일부터 2020년 1월 1일까지의 데이터는 이미 패키지에 포함되어 있으므로, download를 False로 설정하겠습니다.
# stock_list의 Symbol 컬럼을 기준으로 2018년 1월 1일부터 2021년 1월 1일까지의 데이터 불러오기
data_list = datasets.load_stock_data_list(stock_list["Symbol"],
start_date = "2016-01-01",
end_date = "2021-01-01",
download = False)
데이터에 저가와 고가 등이 0인 잘못된 레코드가 종종 있기에, 이러한 데이터는 제거해주겠습니다 (추후 버전에서 이러한 데이터를 제거한 결과를 리턴하도록 수정하겠습니다).
data_list = [data.loc[data['Low'] != 0].reset_index(drop = True) for data in data_list]
3. 요일별 등락률 분포 확인
요일별 등락률을 담을 중첩 리스트를 다음과 같이 정의하겠습니다.
# 요일별 등락률을 담을 리스트 초기화
change_list = [[], [], [], [], []]각 요소 리스트는 순서대로 월, 화, 수, 목, 금요일의 등락률을 담겠습니다.
이제 data_list의 data를 순회하면서 change_list를 업데이트해주겠습니다. dt 접근자의 weekday 속성 (1: 월요일, 2: 화요일, 3: 수요일, 4: 목요일, 5: 금요일)과 Close 컬럼을 기준으로 필터링하겠습니다.
# Date의 weekday를 바탕으로 change_list에 저장
for data in data_list:
data["요일"] = data["Date"].dt.weekday # dt.weekday: 날짜 자료형의 요일을 반환
for i in range(5):
change_list[i] += data.loc[data["요일"] == i, "Change"].dropna().tolist()이제 이 결과를 박스플롯으로 시각화해서 비교하겠습니다. y축의 범위를 -0.05와 0.05로 한정해서 1, 2, 3사분위수를 중점적으로 보겠습니다.
# 박스플롯으로 시각화해서 비교
plt.figure(figsize = (10, 6))
plt.boxplot(change_list)
plt.xticks(range(1, 6), ["Mon", "Tue", "Wed", "Thu", "Fri"])
plt.ylim(-0.05, 0.05)
plt.show()[실행 결과]
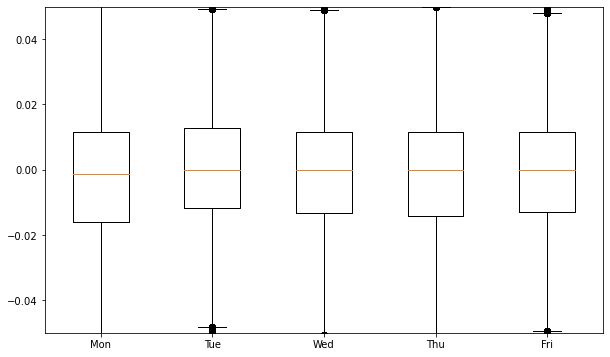
실행 결과를 보면 큰 차이는 아니지만 월요일 박스가 좀 아래에 있고, 금요일 박스가 조금 위에 있음을 알 수 있습니다.
통계량을 계산하여 정확한 수치를 바탕으로 비교해보겠습니다.
# 통계량 확인
result = pd.DataFrame()
for i in range(5):
result = pd.concat([result, pd.Series(change_list[i]).describe()], axis = 1)
result.columns = ["Mon", "Tue", "Wed", "Thu", "Fri"]
display(result.round(3))[실행 결과]
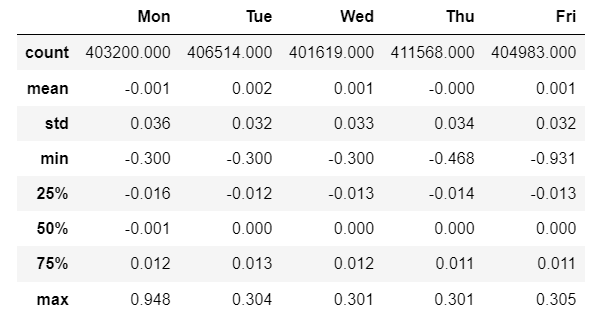
최댓값이 0.3을 넘고 최솟값이 -0.9보다 작은 아웃라이어가 섞여 있지만, 전반적으로 0에 가깝고 요일별 큰 차이가 잘 보이지 않습니다.
4. 월요일에 매수해서 금요일에 매도하는 전략 검증
이번에는 qspy 패키지를 이용하여 월요일에 매수해서 금요일에 매도했을 때의 전략을 검증하겠습니다.
월요일 시가에 매수해서 금요일 종가에 매도했을 때의 수익률과 월요일 종가에 매수해서 금요일 종가에 매도했을 때의 수익률을 각각 ror_list_OC와 ror_list_CC에 저장하겠습니다.
여기서 OC는 Open, Close를, CC는 Close, Close를 의미합니다.
# 수익률 목록 계산: 월요일 시가 - 금요일 종가, 월요일 종가 - 금요일 종가
ror_list_OC = []
ror_list_CC = []
for data in data_list:
buy_arr, sell_arr = calendar_effect.week_effect(data, buy_weekday = 0, sell_weekday = 4, date_col = "Date")
ror_list_OC += ror_buy_and_sell(data, buy_arr, sell_arr, buy_col = "Open", sell_col = "Close")
ror_list_CC += ror_buy_and_sell(data, buy_arr, sell_arr, buy_col = "Close", sell_col = "Close")객관적인 비교를 위해, 임의의 시점에서 매수해서 4영업일 후에 매도했을 때의 수익률도 계산하겠습니다.
# 임의의 시점에서 매수해서 4영업일 후에 매도했을 때의 수익률 계산
ror_list_random_OC = []
ror_list_random_CC = []
for data in data_list:
buy_arr = np.zeros(len(data), dtype = bool)
buy_idx = np.random.choice(range(len(data)), int(len(data) / 5))
buy_arr[buy_idx] = True
ror_list_random_OC += ror_buy_and_hold(data, 4, buy_arr, buy_col = "Open", sell_col = "Close")
ror_list_random_CC += ror_buy_and_hold(data, 4, buy_arr, buy_col = "Close", sell_col = "Close")
이제 네 개의 수익률 목록을 박스플롯으로 시각화해서 비교하겠습니다.
# 박스플롯으로 시각화해서 비교
plt.boxplot([ror_list_OC, ror_list_CC, ror_list_random_OC, ror_list_random_CC])
plt.xticks(range(1, 5), ["MF-OC", "MF-CC", "random-OC", "random-CC"])
plt.ylim(-0.1, 0.1)
plt.show()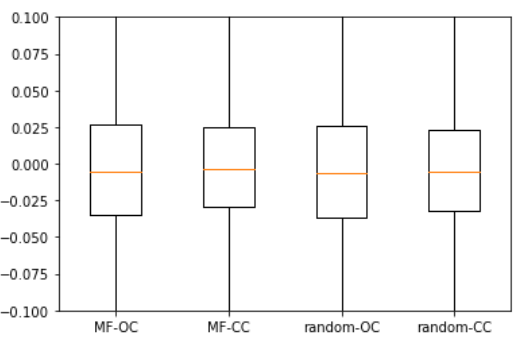
통계량을 계산하여 정확한 수치를 바탕으로 비교해보겠습니다.
# 통계량 확인
result = pd.Series(ror_list_OC).describe()
result = pd.concat([result, pd.Series(ror_list_CC).describe()], axis = 1)
result = pd.concat([result, pd.Series(ror_list_random_OC).describe()], axis = 1)
result = pd.concat([result, pd.Series(ror_list_random_CC).describe()], axis = 1)
result.columns = ["MF-OC", "MF-CC", "random-OC", "random-CC"]
display(result.round(3))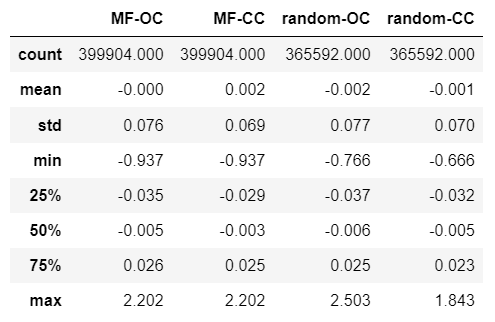
평균과 중위수, 1사분위수 등 어느 수치를 보더라도 임의의 시점에 매수해서 4영업일 후에 매도하는 것과 큰 차이가 없음을 알 수 있습니다.
정리하면 월요일에 매수해서 금요일에 매도한다는 전략은 무의미함을 알 수 있습니다.
실험 코드
실험에 사용한 전체 코드는 아래와 같습니다.
수집하고 싶은 금융 데이터나 실험하고 싶은 퀀트 관련 아이디어가 있으면 댓글로 남겨주세요!
관련 포스팅을 준비하도록 하겠습니다!

출처: https://gils-lab.tistory.com/41 [GIL's LAB]
'퀀트 투자 > 실험 일지' 카테고리의 다른 글
| 실험 10. 상승 반전형 단일 캔들 패턴에 따른 수익률 비교 (0) | 2021.12.29 |
|---|---|
| 실험 9. 평균 회귀 전략 검증 (feat. 첫 성공?) (0) | 2021.11.18 |
| 실험 8. 캔들 패턴 분석: (1) 상승장악형, 하락장악형 (0) | 2021.11.17 |
| 실험 7. 골든크로스와 데드크로스의 효과 분석 (2) | 2021.10.05 |
| 실험 6. 증권사의 의견에 따라 투자해보기 (1) | 2021.10.03 |




